Elliptic-curve cryptography (ECC)
Math
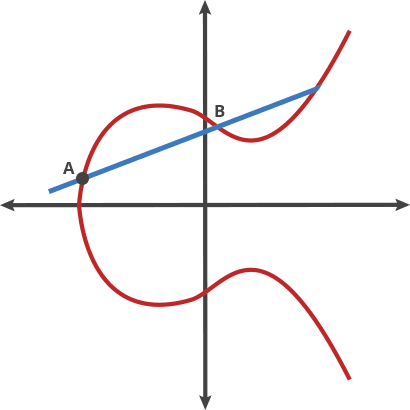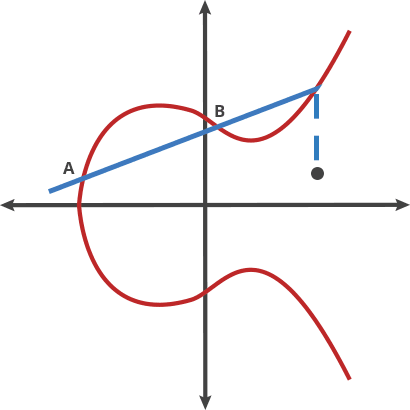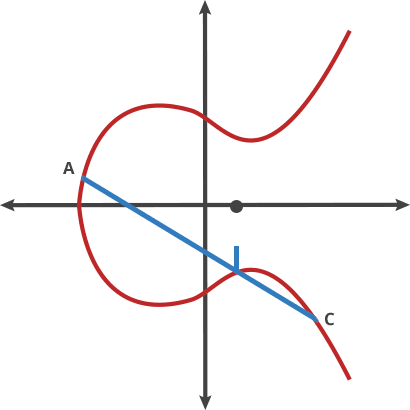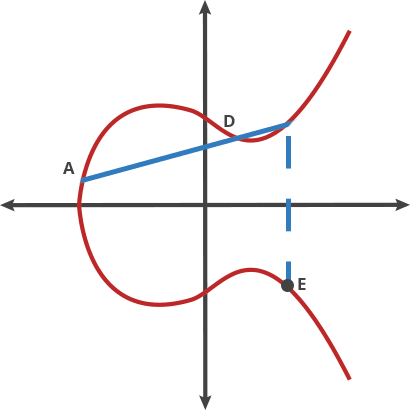
- where is public point/key on the curve, is an integer (private key). is the common generation point.
- Its security relies on the difficulty of calculating given starting point and ending point
- To crack it, only brute force works, whose time complexity is O(number of choices) or O(2^{number of digits of key}) i.e. exponential complexity
- > breaking a 228-digit ECC requires energy to boil all water on the earth
Practical
- The U.S. National Security Agency (NSA) allows their use for protecting information classified up to top secret with 384-bit keys.
Terminologies
- ECDH: Diffie-Hellman key exchange method using specifically elliptic curves;
- ECDSA: DSA (Digital Signature Algorithm) using specifically elliptic curves;
- EdDSA: Edwards-curve Digital Signature Algorithm is a digital signature scheme using a variant of Schnorr signature based on twisted Edwards curves.
- Curve25519: one of the curve
Reference
NIST Curve的后门阴谋论
- > Some of the more skeptical cryptographers in the world now have a general distrust for NIST itself and the standards it has published that were supported by the NSA. Almost all of the widely implemented elliptic curves fall into this category. There are no known attacks on these special curves, chosen for their efficient arithmetic, however bad curves do exist and some feel it is better to be safe than sorry. There has been progress in developing curves with efficient arithmetic outside of NIST, including curve 25519 created by Daniel Bernstein (djb) and more recently computed curves by Paulo Baretto and collaborators, though widespread adoption of these curves are several years away.
1 page links here
Public-Key Cryptography
Elliptic-curve cryptography (ECC) ED25519